Berechnungen und Informationen zu Turbinen, Generatoren, Schalttafeln und Akku-Anlagen
In den Artikeln "2. Die Francis-Turbine der »Wilhelmsmühle« in Züschen" und "4. Der Drehstrom-Klauenpol-Generator der »Wilhelmsmühle« in Züschen" dieser Internetseiten zur elektrischen Energieerzeugung an der nordhessischen Elbe werden Berechnungen erwähnt, die zum besseren Verständnis in den folgenden Abschnitten 1 – 5 erläutert werden. Im Artikel "6. Die Haupt-Schalttafel des »Ritterguts Züschen« für den Strom aus der Wilhelmsmühle«" werden Begriffe aus der Messtechnik verwendet, die erklärungsbedürftig im Abschnitt 6 vorgestellt werden. Und zum Abschluss werden in den Abschnitten 7 und 8 Details zur Energie-Speicherung und -Nutzung der Blei-Akkumulatoren sowie zu den chemischen Vorgängen bei der Ladung und Entladung der Blei-Akkumulatoren vorgestellt.
1. Berechnung der Turbinenleistung
Die mindestens drei aufeinander folgenden Turbinen der "Wilhelmsmühle" trieben ab 1893 zunächst einen zeitgemäßen Gleichstrom-Dynamo und ab ca. 1898 die auf der IEA 1891 in Frankfurt vorgestellte Drehstromtechnik mit einem Generator über Flachriemen und ein Vorgelege an, zwischen 1893 – 1907 zusätzlich über ein Kegelradgetriebe. Damit konnte in einem gewissen Bereich die Anpassung der Turbinendrehzahl an die erforderliche Dynamo- bzw. Generator-Drehzahl erfolgen, gleich ob es um leistungs- oder frequenzoptimale Drehzahlen ging. Bei größeren bis großen Leistungen ist der Direktantrieb Mittel der Wahl, erstens weil hohe Leistungen bzw. Drehmomente nicht mehr über Flachriemen oder auch Keilriemen übertragen werden können, zweitens um zwangsläufig entstehenden lastabhängigen Schlupf auszuschalten.
Die Leistung einer Wasserturbine wird nach der Formel PT = ηT * ρH2O * g * h * V berechnet. Hierin bedeuten
- ηT den Turbinenwirkungsgrad ohne Berücksichtigung der Rohr-Reibungsverluste, welcher bei fehlender Angabe wie bei der Francis-Turbine mit 0,9 angesetzt werden kann,
- ρH2O (sprich: rho H2O) die Dichte des Wassers mit üblicherweise 1 = 1.000 kg/m3,
- g die Erdbeschleunigung mit 9,81 m/s2,
- h die wirksame Wasserfallhöhe in m mit Berücksichtigung der Rohrreibung,
- V das Schluckvermögen (der Wasserdurchfluss) in m3/s.
Für die Francis-Turbine ist in der Zeichnung zum Umbau in 1907 der minimale Oberwasserspiegel, also der Stand des Wassers vor dem Einlauf in die Turbine, mit 203,037 m ü.N.N. (über Normal-Null = durchschn. Meereshöhe) angegeben, der Unterwasserspiegel mit 197,967 m ü.N.N. Hieraus resultiert eine minimale Fallhöhe von 5,07 m, von der hier geschätzt 0,27 m abgezogen werden und eine wirksame Fallhöhe von 4,80 m ergeben. In den Antrags- und Genehmigungsunterlagen ist die maximale Entnahme- und Wiederzuleitungsmenge mit 565 Litern je Sekunde, also 0,565 m3/s angegeben. Dies führt unter Weglassung der jeweiligen Dimensionen zur Leistungsberechnung mit
PT = 0,9 * 1 * 9,81 * 4,80 * 0,565 = 23,9 kW (ehemals ca. 33 PS)
In der Zeichnung zum Umbau in 1907 sind die Fallhöhe mit 5,70 m, der Wasserdurchfluss mit 560 l/s und die Leistung mit 35,3 PS entspr. knapp 26 kW angegeben. Da sich an der Physik außer Bezeichnungen und Dimensionen nichts geändert hat und heutige Turbinen sicherlich eine höhere Effizienz haben bleibt für die Differenz zu unserer Rechnung, dass mit der Angabe 5700 mm die Fallhöhe bis zum höchsten Oberwasserspiegel von 203,667 m ü.N.N. angesetzt wurde. Dies kann aber nur gelten, wenn der Zufluss in den Stauweiher auch 560 l/s beträgt, der OW-Spiegel also auf gleicher Höhe verbleibt.
2. Berechnung der Polzahlen von Synchronmaschinen
 Wieviel Pole benötigt ein Generator bei einer angegebenen Drehzahl von 750 Umdrehungen je Minute (750 U/min oder auch 750 min-1) für die Erzeugung einer Frequenz von 50 Hertz (Hz)? Dies sind, wie am Beispiel des auch hier klein wiedergegebenen Drehstromdiagramms im Artikel "4. Der Drehstrom-Klauenpol-Generator ...." für 40 Millisekunden zu erkennen ist, unabhängig von einphasigem Wechselstrom und dreiphasigem Drehstrom, in jeder Sekunde 50 volle Schwingungen von Null über positiven Maximalwert und weiter über Null und negativen Maximalwert bis wieder zu Null (s. Grafik rechts bzw. oben, *1).
Wieviel Pole benötigt ein Generator bei einer angegebenen Drehzahl von 750 Umdrehungen je Minute (750 U/min oder auch 750 min-1) für die Erzeugung einer Frequenz von 50 Hertz (Hz)? Dies sind, wie am Beispiel des auch hier klein wiedergegebenen Drehstromdiagramms im Artikel "4. Der Drehstrom-Klauenpol-Generator ...." für 40 Millisekunden zu erkennen ist, unabhängig von einphasigem Wechselstrom und dreiphasigem Drehstrom, in jeder Sekunde 50 volle Schwingungen von Null über positiven Maximalwert und weiter über Null und negativen Maximalwert bis wieder zu Null (s. Grafik rechts bzw. oben, *1).
Zu erkennen ist bei den obigen Daten, dass die Drehzahl je Minute angegeben ist, die Frequenz aber in Vollschwingungen je Sekunde. Also muss die Zahl 60 für die Zahl der Sekunden je Minute in die Rechenformel, denn 50 Hertz bedeutet 3000 Vollschwingungen je Minute (50 * 60 = 3.000). Und da bei jeder Umdrehung des Rotors innerhalb der Statorwicklung die Magnetfeldlinien aller Nord- und Südpole an jedem Wicklungsteil vorbei drehen, kann die Formel nur lauten p = 60 * f / n. Hierin bedeuten
- p die Polpaarzahl, also die Summe der Nord- und Südpole einer Maschine, denn ein einzelner Nord- oder Südpol ist nicht möglich,
- 60 die Zahl der Sekunden je Minute,
- f die Frequenz in Hz,
- n die Zahl der Umdrehungen je Minute (U/min).
Für den Generator sind auf dessen Leistungsschild eine Frequenz von 50 Hz und eine Drehzahl von 750 U/min angegeben. Die erforderliche Anzahl der Polpaare kann also berechnet werden mit
p = 60 * 50 / 750 = 4
und ist bei dessen Betrachtung von rechts und links auch gut sichtbar: Es ragen von jeder Seite vier "Klauen" in den Luftspalt zwischen Stator und Rotor, also je vier Nord- und Südpole. Beim Oerlikon-Generator aus 1891 ist das Zählen schon mühsamer.
Obige Formel gilt unabhängig von der Frequenz nicht nur für Drehstrom-Synchron-Generatoren, sondern auch für Synchron- und Asynchron-Motoren und erklärt bei unserem europäischen und darüber in großen Teilen der Welt verbreiteten 50-Hz-Netz auch, warum keine Motoren für 1.200, 2.100 oder gar 3.700 U/min erhältlich sind. Die unsichtbare Rotation des im Stator erzeugten Magnetfelds erfolgt immer synchron mit der Frequenz.
- Ein hiervon unabhängig erzeugtes Magnetfeld im Rotor der Synchronmotoren führt nach Anlauf immer zu einem synchronen Lauf des Motors. Aus dem Tritt kann er nur bei Überlastung, also zu hoher Drehmomentanforderung durch die angetriebene Arbeitsmaschine kommen.
- Bei Asynchronmotoren erfolgt die Feldbildung des Rotors durch die hohen Ströme der in ihm immer kurzgeschlossenen Wicklung. Die zumeist vorkommenden Kurzschlussläufer haben immer eine kurzgeschlossene Läuferwicklung (Rotorwicklung) und erfordern beim Einschalten höhere Anlaufströme.
Bei Schleifringläufern wird deren Rotorwicklung über Schleifringe nach außen zu einem dreiphasigen Widerstand geführt, dessen wirksamer Widerstand beim Anlauf stufenweise verringert, zum Schluss kurzgeschlossen wird und einen niedrigeren Anlaufstrom hat. Der Widerstand kann bei richtiger Auslegung und ggf. Kühlung auch zur verlustbehafteten Drehzahleinstellung benutzt werden. Beide Ausführungsformen laufen mit ihren Rotoren selbst bei geringster Belastung nie mit der Synchrondrehzahl des speisenden Netzes, sondern haben dagegen immer einen Schlupf. Denn ohne diesen würde im Rotor kein magnetisches Feld erzeugt, welches durch die Rotation des Feldes im Stator mitgenommen wird.
Die Synchron-Drehzahlen in Abhängigkeit von der Polpaarzahl betragen demnach für die gängigen Netze
| p = Polpaare | Synchrondrehzahl (U/min) bei 50 Hz |
Synchrondrehzahl (U/min) bei 60 Hz |
||
| 1 | 3.000 | 3.600 | ||
| 2 | 1.500 | 1.800 | ||
| 3 | 1.000 | 1.200 | ||
| 4 | 750 | 900 | ||
| usw. usw. | ||||
| 10 | 300 | 360 | ||
| 12 | 250 | 300 | ||
| 16 | 187,5 | 225 |
Selbstverständlich ließe sich diese Tabelle beliebig verlängern und verbreitern, aber verbreitet sind weder andere Frequenzen noch höhere Polpaarzahlen. Der weltweit erste Drehstrom-Generator, gebaut für die IEA 1891 in Frankfurt und auch in Klauenpolversion wie unser TMK-Exponat, hatte auch 16 Polpaare wie die Angabe in der letzten Zeile obiger Tabelle, drehte allerdings nur 150 Umdr./min und erzeugte somit eine Frequenz von nur 40 Hz.
3. Zusammenhang zwischen Leistung, Drehmoment und Drehzahl
Höhere Leistung erfordert bei gleichbleibenden Drehzahlen höhere Drehmomente, denn analog zur Berechnung der Leistung bei einer linearen Bewegung P = F * v ergibt die Winkelgeschwindigkeit ω (gr. Omega) einer Drehbewegung und das Drehmoment M (Produkt aus Kraft in Newton, welche senkrecht zur gedachten Hebellänge in Meter der sich drehenden Turbinenwelle wirkt) sowohl bei der Turbine als auch dem Generator deren Leistung P in Kilowatt. Für Praktiker abgekürzt: P = (M * n) / 9550 ! Das Drehmoment M wird in Newtonmeter (Nm), die Drehzahl n in U/min eingegeben, die Zahl 9550 fasst alle Umrechnungsparameter aus der wissenschaftlichen Berechnung wie π (griech. Pi), die Zahl 2 , Leistung in Kilowatt (kW) sowie Maßangaben und Zeit zusammen. Und höhere Leistung ist bei längerem Hebelarm einer Drehbewegung leichter zu realisieren. Sagte angeblich schon Archimedes im 3. Jh. v. Chr., hier frei zitiert: Gebt mir einen Fixpunkt im All und ich werde die Welt aus ihren Angeln heben. Klar, mit einem sehr langen Hebel würde Archimedes dies schaffen, aber den Fixpunkt, den langen Hebel und dessen Steifigkeit (phys./mech.: dessen Widerstandsmoment) gibt es nicht und wird es auch nie geben!
Jetzt könnte man angesichts des großen Durchmessers unseres Drehstrom-Generators meinen, dass dieser eine hohe Leistung hat. Nein, er hat aus heutiger Sicht, also unter Berücksichtigung des Blindleistungsfaktors cos φ (griech. phi) von 0,8 (s. Abschnitt 5 unten), bei dieser großen Masse nur eine elektrische Leistung von 16 kW bei einer Drehzahl von 750 U/min. Also wirkt nach obiger Formel ohne Berücksichtigung eines Wirkungsgrades an seiner Welle ein Drehmoment von
M = (P * 9550) / n = (16 * 9550) / 750 = 204 Nm.
Da vielen Besuchern unseres TMK der Begriff Newton für eine Kraft nichts sagt: Das Verhältnis der Kraft in Newton (N) zur Kraft in der vertrauten Maßeinheit Kilogramm (kg), welche nur für die Masse eines Körpers wie z.B. der des menschlichen gilt, beträgt 9,81. Unsere Masse bleibt auf dem Mond, dem Mars oder im schwerelosen Weltall stets die Gleiche, aber die Gewichtskraft unterscheidet sich durch die unterschiedlichen Anziehungskräfte des Himmelskörpers, dem wir uns nähern oder auf dem wir sogar sind: Für die Erde gilt eine Beschleunigung von 9,81 m/s2, für den Mond 1,62 und den Mars 3,72. Also wirken auf der Erde an der Generatorwelle der WKA "Wilhelmsmühle" aufgerundet 21 kgm. Die Kraft, mit der ein ein Meter langer Hebel mit 250 U/min gedreht werden müsste, betrüge nach der veralteten Dimension also nur 21 kg. Wirklich nicht viel für einen kurzen Moment, aber auf Dauer den Menschen überlastend!
4. Berechnung der Leistung aus Spannung und Strom
Beim Artikel zum Drehstrom-Generator sind zur Erklärung der Verkettung drei Spannungszeiger U1N, U2N und U3N dargestellt, die Strangspannungen genannt werden, hier rechts wiederholt. Sie haben ihren Ursprung in einem gemeinsamen Sternpunkt und rotieren linksläufig um diesen. Dabei beschreiben sie mit ihren Spitzen fortlaufend einen Kreis mit 360° und haben zueinander also einen Winkelabstand von 120°. Wenn jeder der drei gleich langen Zeiger eine Spannung von knapp 290 V repräsentieren würde, wäre die Spannung zwischen den Spitzen von U2N und U3N, also U23 aufgrund der dargestellten Winkelfunktionen um den Faktor √3 = 1,73 höher und entspräche der verketteten Generatorspannung 500 V der "Wilhelmsmühle" in Züschen (s. Grafik rechts bzw. oben, *1).
 Auf dem Leistungsschild des Drehstrom-Klauenpol-Generators war zur Herstellungszeit noch keine Leistungsangabe vorgesehen, lediglich Spannung U und abzugebender Strom I sind mit 500 V und 3 * 23 A genannt. Hier handelt es sich um die Spannungen der drei Leiter L1, L2 und L3 gegeneinander. Diese werden entsprechend dem Diagramm unter obigem Abschnitt 2 mit U12, U23 und U31 bezeichnet und betragen laut Leistungsschild jeweils 500 V. Den Strom dreifach für die drei Leiterströme anzugeben verweist auf den Beginn der Drehstromtechnik für viele Elektrotechniker und erscheint heute sinnlos, denn ein Drehstrom-Generator wurde ja dafür entwickelt und gebaut!
Auf dem Leistungsschild des Drehstrom-Klauenpol-Generators war zur Herstellungszeit noch keine Leistungsangabe vorgesehen, lediglich Spannung U und abzugebender Strom I sind mit 500 V und 3 * 23 A genannt. Hier handelt es sich um die Spannungen der drei Leiter L1, L2 und L3 gegeneinander. Diese werden entsprechend dem Diagramm unter obigem Abschnitt 2 mit U12, U23 und U31 bezeichnet und betragen laut Leistungsschild jeweils 500 V. Den Strom dreifach für die drei Leiterströme anzugeben verweist auf den Beginn der Drehstromtechnik für viele Elektrotechniker und erscheint heute sinnlos, denn ein Drehstrom-Generator wurde ja dafür entwickelt und gebaut!
Im Drehstromsystem wird die Leistung aus Vereinfachungsgründen mit P = U * I * √3 berechnet. Tatsächlich geht es bei der Leistungsberechnung aber um die Spannungen der drei Einzelleiter L1, L2 und L3 gegen ihren gemeinsamen Ursprung, den keineswegs immer herauszuführenden Sternpunkt N mit den drei Strangspannungen U1N, U2N und U3N und deren jeweiligen Strömen I1, I2 und I3. Diese drei Strangleistungen werden addiert und führen zur Gesamtleistung. In der Leiterspannung ist gegenüber der Strangspannung bereits der Faktor √3 enthalten, daher kommt anstelle des Faktors 3 bei der Ermittlung der Gesamtleistung aus den drei Strangleistungen auch hier nur √3 zum Tragen.
Die auf dem Leistungsschild nicht angegebene Generatorleistung könnte also berechnet werden mit
P = 380 * 23 * √3 = 19,92 kW
wenn nicht der Blindstrom wäre, den der Generator zur Magnetisierung der Statoren angeschlossener Motoren liefern muss. Und dies musste er auch damals schon, die Kennzeichnung war aber noch nicht in die Normung eingezogen. Korrekt wäre zunächst also, die Leistung dieses Generators mit 19,92 kVA anzugeben, aufgerundet 20 kVA. Dies könnte sich in der Typbezeichnung im Leistungsschild rechts oben mit WNd20 widerspiegeln.
5. Zusammenhang zwischen Wirkleistung, Blindleistung und Scheinleistung
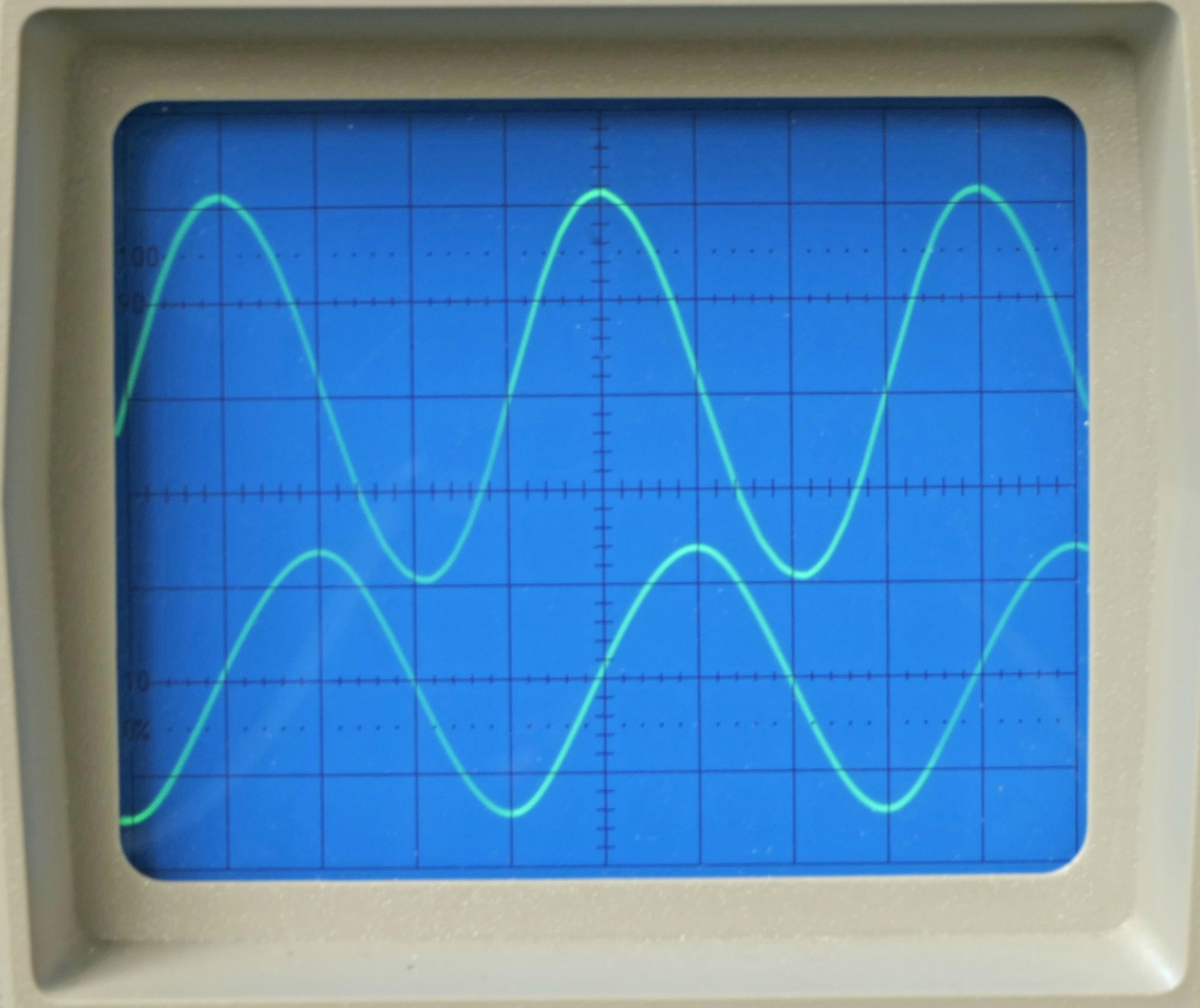 Jede Zuschaltung eines Stroms verursacht den Aufbau eines Magnetfeldes, gleich ob in einem linear geführter Draht (z.B. ein Leiterseil einer Freileitung) oder – das Magnetfeld noch verstärkend – in einer Spule bzw. Wicklung. Bei der Strom-Abschaltung wiederum verursacht das dann zusammenbrechende Magnetfeld die Induktion einer Spannung in Draht bzw. Leiterseil (Prinzip der elektromagnetischen Induktion, unabhängig voneinander entdeckt durch den Engländer Michael Faraday, den Amerikaner Joseph Henry und den Dänen Hans Christian Oersted Anfang der 1830-er Jahre). Bei einem Wechselstrom von z.B. 50 Hz erfolgt dieser Magnetfeldauf- und abbau 100 mal in der Sekunde wegen der wechselnden Stromrichtung und verursacht damit einen frequenzabhängigen Widerstand gegen den Wechselstrom, den Blindwiderstand. Ohne Berücksichtigung des Ohm´schen Widerstands dieses Drahtes in einer Wicklung folgt der Wechselstrom der treibenden Spannung um 90°el später in seiner Form, idealerweise der Sinuskurve einer Vollschwingung von 360°el. Das Strommaximum erreicht er also bei 50 Hz erst 5 Millisekunden (ms) nach dem Spannungsmaximum usw. usw., bis nach 20 ms, also einer Vollschwingung, das Spannungsminimum auf der Nulllinie und das Strommaximum im Negativbereich erreicht sind. Dieser Strom bedarf keiner Wirkarbeit in der treibenden Arbeitsmaschine, belastet aber dennoch den Generator, einen Transformator und die Leitungen, er pendelt also ständig hin und her. In neben- bzw. obenstehendem Oszilogramm, erstellt an unserem TMK-Modell für ohmsche, induktive und kapazitive Belastungen, ist dies mit der treibenden Wechselspannung in der oberen Kurve und dem daraus resultierenden Strom in der unteren Kurve gut zu erkennen (in der horizontalen Auflösung 5 ms je Kästchen, s. Bild rechts bzw. oben).
Jede Zuschaltung eines Stroms verursacht den Aufbau eines Magnetfeldes, gleich ob in einem linear geführter Draht (z.B. ein Leiterseil einer Freileitung) oder – das Magnetfeld noch verstärkend – in einer Spule bzw. Wicklung. Bei der Strom-Abschaltung wiederum verursacht das dann zusammenbrechende Magnetfeld die Induktion einer Spannung in Draht bzw. Leiterseil (Prinzip der elektromagnetischen Induktion, unabhängig voneinander entdeckt durch den Engländer Michael Faraday, den Amerikaner Joseph Henry und den Dänen Hans Christian Oersted Anfang der 1830-er Jahre). Bei einem Wechselstrom von z.B. 50 Hz erfolgt dieser Magnetfeldauf- und abbau 100 mal in der Sekunde wegen der wechselnden Stromrichtung und verursacht damit einen frequenzabhängigen Widerstand gegen den Wechselstrom, den Blindwiderstand. Ohne Berücksichtigung des Ohm´schen Widerstands dieses Drahtes in einer Wicklung folgt der Wechselstrom der treibenden Spannung um 90°el später in seiner Form, idealerweise der Sinuskurve einer Vollschwingung von 360°el. Das Strommaximum erreicht er also bei 50 Hz erst 5 Millisekunden (ms) nach dem Spannungsmaximum usw. usw., bis nach 20 ms, also einer Vollschwingung, das Spannungsminimum auf der Nulllinie und das Strommaximum im Negativbereich erreicht sind. Dieser Strom bedarf keiner Wirkarbeit in der treibenden Arbeitsmaschine, belastet aber dennoch den Generator, einen Transformator und die Leitungen, er pendelt also ständig hin und her. In neben- bzw. obenstehendem Oszilogramm, erstellt an unserem TMK-Modell für ohmsche, induktive und kapazitive Belastungen, ist dies mit der treibenden Wechselspannung in der oberen Kurve und dem daraus resultierenden Strom in der unteren Kurve gut zu erkennen (in der horizontalen Auflösung 5 ms je Kästchen, s. Bild rechts bzw. oben).
 So wie induktive Ströme den Spannungen nacheilen ist das auch mit den Leistungen, beim jeweiligen Objekt zusammengesetzt aus unterschiedlichem induktiven und ohmschen Anteil. Ein leer laufender Motor benötigt Wirkstrom nur zur Deckung seiner eigenen Verluste wie Lagerreibung, Lüfter zur Kühlung und selbstverständlich den ohmschen Verlusten in der Wicklung und damit Erwärmung, der induktive Anteil durch die Magnetfeldbildung kann überwiegen. Bei einem stark belasteten Motor fällt der induktive Anteil nicht mehr so stark ins Gewicht, kann aber keineswegs vernachlässigt werden. Daher wurde in der Normung für Generatoren und Transformatoren ein Leistungsfaktor cos φ (griech. phi) von 0,8 als realistischer Mittelwert des Verhältnisses der Wirk- zur Scheinleistung festgelegt.
So wie induktive Ströme den Spannungen nacheilen ist das auch mit den Leistungen, beim jeweiligen Objekt zusammengesetzt aus unterschiedlichem induktiven und ohmschen Anteil. Ein leer laufender Motor benötigt Wirkstrom nur zur Deckung seiner eigenen Verluste wie Lagerreibung, Lüfter zur Kühlung und selbstverständlich den ohmschen Verlusten in der Wicklung und damit Erwärmung, der induktive Anteil durch die Magnetfeldbildung kann überwiegen. Bei einem stark belasteten Motor fällt der induktive Anteil nicht mehr so stark ins Gewicht, kann aber keineswegs vernachlässigt werden. Daher wurde in der Normung für Generatoren und Transformatoren ein Leistungsfaktor cos φ (griech. phi) von 0,8 als realistischer Mittelwert des Verhältnisses der Wirk- zur Scheinleistung festgelegt.
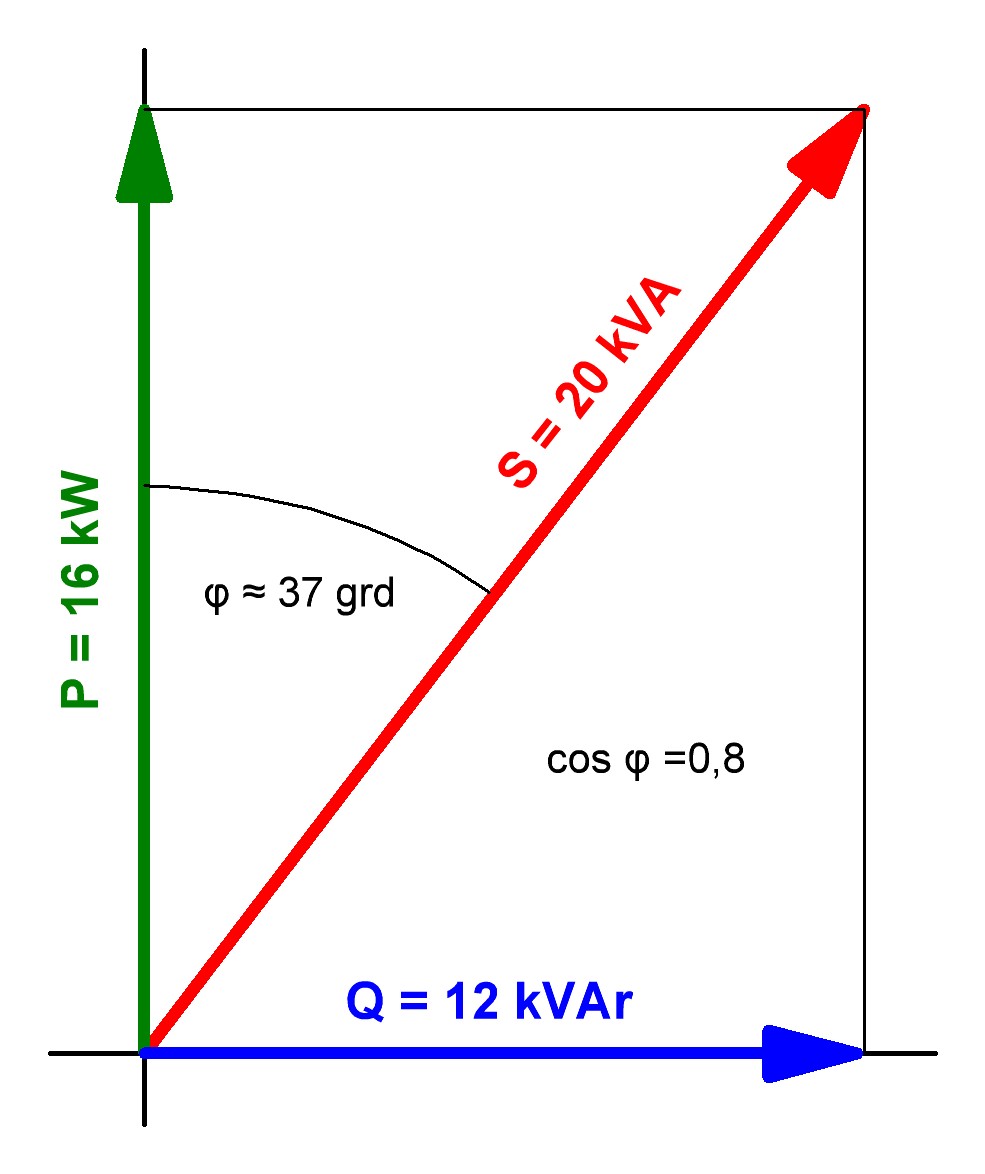
Im links bzw. oben wiedergegebenen rechteckigen Dreieck aus Wirkleistung P (senkrechte Achse, grün) und Projektion der Blindleistung Q (blau) nach oben (waagerechte dünne Linie) ist der Winkel der Ankathete zur Hypotenuse mit dem Winkel φ dargestellt. Dieser definiert mit seinem Cosinus – der Leser dieser Seite erinnert sich sicherlich gut an Trigonometrie innerhalb der vielen seinerzeitigen Schülern verhassten Mathematik – den Wirkanteil P an der Scheinleistung S (rot). Die Blindleistung Q (blau) ist dann die Gegenkathete im Dreieck (s. Grafik oben, *1).
Für den Drehstrom-Generator wurde im vorigen Abschnitt eine Scheinleistung S von 20 kVA errechnet. Dessen Wirkleistung könnte dann betragen
P = S * cos φ = 20 * 0,8 = 16 kW
Es könnte aber – angesichts der seinerzeit noch fehlenden Normung und auch ungewöhnlichen Dimensionen sowie Materialmassen unseres TMK-Exponats – auch sein, dass mit der Multiplikation aus den Generatordaten 500 V und 23 A sowie der √3 tatsächlich die Wirkleistung gemeint war. Dann würde die Scheinleistung betragen
S = P / cos φ = 20 / 0,8 = 25 kVA
Fachleute wussten mit Sicherheit um die Bedeutung von Wirk- und Blindleistung, denn diese Thematik wurde von M. O. v. Dolivo-Dobrowolsky auf dem "Internationalen Elektrotechniker-Congress Frankfurt a. Main 1891" vor prominentem Publikum vorgetragen und auch publiziert:
"Dieser um 90° gegen seine Spannung verschobene Strom repräsentiert keine geleistete Arbeit, sondern nur eine oscillierende Energie, da er die Hälfte der Zeit mit seiner Spannung, wie in einer Dynamo[maschine], die andere Hälfte der Zeit gegen seine Spannung gerichtet ist. Dieser wattlose Strom, da er ausschließlich die Magnetisierung zu besorgen hat, soll Erregungsstrom genannt werden. ..... Einen Strom, der keine Verschiebung gegen die Spannung hat und somit vollauf dem Energiekonsum resp. der Leistung entspricht, schlage ich vor Wattstrom zu nennen" (Quelle *2).
Nun, es wurden die Begriffe Blindstrom und Wirkstrom daraus, aber das Thema war damit in der Fachwelt bekannt und hätte zur Normung und vor allem Anwendung bei Generatoren, Transformatoren und Leitungen führen sollen. Diese Lösung würde zwar nicht alleinentscheidend zur gestellten Aufgabe der Leistungsbestimmung passen, aber der Leistungsbestimmung des Drehstrom-Generators mit 25 kVA / 20 kW der Francis-Turbine mit ihren knapp 24 kW in der "Wilhelmsmühle" ist sie damit erheblich näher gekommen (s. Abschnitt 1).
 Sicherlich für einen Nicht-Elektrotechniker wirklich nicht einfach, aber dafür hat die Hochschulgruppe des VDE-Bezirksvereins Kassel e.V. am Fachbereich Elektrotechnik/Informatik der Universität Kassel eine Lösung parat, die nicht ganz so korrekt ist wie sie sein sollte, schon gar nicht technisch-wissenschaftlich wie es sich für Studenten und ausgebildete Ingenieure der Elektrotechnik gehört! Aber dafür ist sie insbesondere abends in der Hauptstadt der Waschbären eine sehr einleuchtende Alternative. Wenn man lange genug hinschaut sieht man immer mehr dieser putzigen Wesen, der liefernde Schankwirt hat aber auch eine durchaus passende Erläuterung: Schaum ist auch Bier und keineswegs Blindleistung!
Sicherlich für einen Nicht-Elektrotechniker wirklich nicht einfach, aber dafür hat die Hochschulgruppe des VDE-Bezirksvereins Kassel e.V. am Fachbereich Elektrotechnik/Informatik der Universität Kassel eine Lösung parat, die nicht ganz so korrekt ist wie sie sein sollte, schon gar nicht technisch-wissenschaftlich wie es sich für Studenten und ausgebildete Ingenieure der Elektrotechnik gehört! Aber dafür ist sie insbesondere abends in der Hauptstadt der Waschbären eine sehr einleuchtende Alternative. Wenn man lange genug hinschaut sieht man immer mehr dieser putzigen Wesen, der liefernde Schankwirt hat aber auch eine durchaus passende Erläuterung: Schaum ist auch Bier und keineswegs Blindleistung!
6. Die Messprinzipien "Drehspule" und "Dreheisen" mit Shunt , Vorwiderstand und Wandlern als Messbereichserweiterung
Bei den im Artikel "6. Die Haupt-Schalttafel des »Ritterguts Züschen« für den Strom aus der »Wilhelmsmühle«" vorgestellten Messgeräten beruht das Messprinzip auf Magnetfeldbildungen und sich gegenseitig abstoßender Wirkung. Bei den Messgeräten Nr. 1 und 4 wurden die Fachbegriffe Drehspul- bzw. Dreheiseninstrument, Shunt (Nebenwiderstand) und Spannungswandler verwendet. Ohne in die Tiefe zu gehen hier vorab eine kurze Erläuterung dieser Begriffe, weil im Teilgebiet Messtechnik des Sammlungsgebiets Elektrische Energietechnik bisher keine detaillierten Erklärungen veröffentlicht wurden:
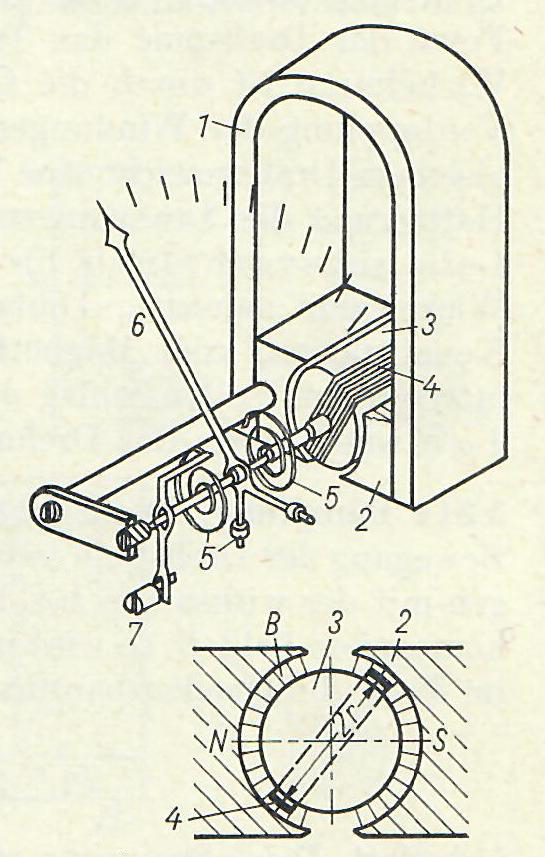
Die Grafik links bzw. oben (Quelle*3 ) zeigt ein typisches Drehspulmessinstrument, welches je nach Erweiterung durch Shunt und Vorwiderstände (s. weiter unten) für Ströme und Spannungen in weiten Messbereichen verwendet wurde, teilweise noch wird. Innerhalb eines Hufeisenmagneten "1" mit Polschuhen "2" ist auf einem Polkern "3" eine Drehspule "4" drehbar gelagert. Der Hufeisenmagnet lässt, von seinem Nordpol "N" ausgehend, ein Magnetfeld über den linken Polschuh, den Polkern, damit auch die Drehspule und mit Feldlinien einwirken, welche beim Südpol "S" wieder eintreten. Der Polkern besteht aus Weicheisen, weil dieses Material nicht magnetisierbar ist und die Feldlinien nur hindurchtreten lässt und damit keine dauerhafte Wirkung ausübt. Die Drehspule bekommt die Messgröße Strom oder Spannung durch zwei gegenläufig gewickelte Spiralfedern "5" zugeführt. Auch eine zu messende Spannung ist durch den Spulenwiderstand – und ggf. einen Vorwiderstand – bestimmt immer ein Strom. Die Spiralfedern üben ein sog. Richtmoment auf den drehbaren Polkern und den Zeiger "6" aus, welches durch die Stellschraube "7" so beeinflusst werden kann, dass der Zeiger ohne anliegende Messgröße auf Skalenstellung "0" steht.
Wenn eine Messgröße anliegt, also ein Strom durch die Drehspule "4" fließt, entsteht ein Drehmoment, welches durch die Spiralfedern ausgewogen wird und mit dem Zeiger "6" auf der Skala angezeigt wird. Durch die Form der Polschuhe "2" ist dafür gesorgt, dass die Induktion "B" des Hufeisenmagneten "1" unabhängig vom Drehwinkel des Polkerns "3" und damit auch der Drehspule "4" konstant bleibt und radial gerichtet ist, dargestellt durch die auf die Polkernmitte gerichteten symbolischen Feldlinien. Da also zwei Magnetfelder, das des Hufeisenmagneten und das in der Drehspule durch Stromfluss entstehende, aufeinander einwirken ist die Ausschlagrichtung durch die Stromrichtung bestimmt. Daher können Drehspulinstrumente prinzipiell keine Wechselströme und -spannungen anzeigen, weil bei z.B. 50 Hz in unseren Netzen und damit auch schon bei der WKA "Wilhelmsmühle" die Stromrichtung 100-mal in der Sekunde wechselt. Da kommt das Messwerk aufgrund seiner noch so kleinen Masse der Drehspule mit Polkern, Spiralfedern und Zeiger nicht mit. Ausnahmen bilden Gleichrichterschaltungen vor dem Messwerk, welche einen Mittelwert unterschiedlicher Art anzeigen können.
Die Grafik rechts bzw. oben (Quelle*3 ) 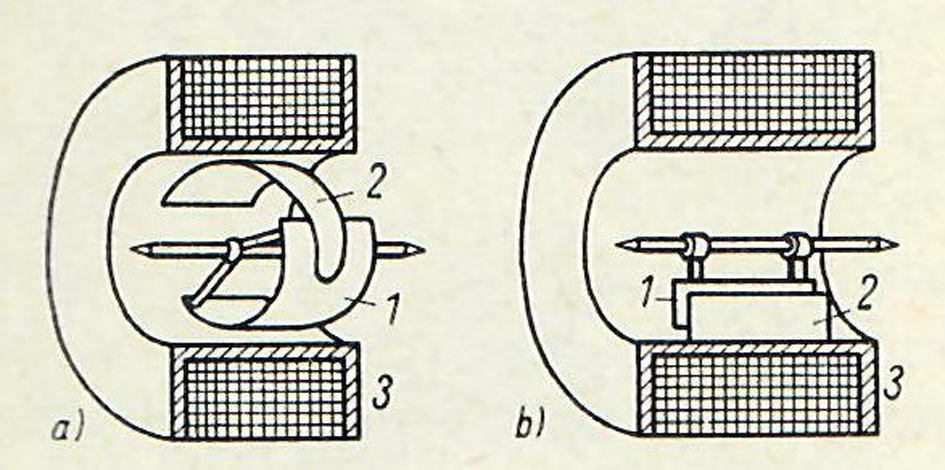 zeigt mit der Anordnung und Form der Bleche in a) ein Mantelkern-, in b) ein Streifenkern-Messwerk. In einer Rundspule ist zentrisch ein drehbares Blech (1 ) angeordnet, welches beim Mantelkern-Messwerk von einem feststehenden Blech (2 ) umgeben ist bzw. dem beim Streifenkern-Messwerk ein feststehender Blechstreifen (2 ) gegenüber steht. Das drehbare Blech ist mit der Zeigerachse verbunden. Durch den die Rundspule durchfließenden Strom werden in jedem Messwerk beide Bleche gleichsinnig magnetisiert, sodass sie sich voneinander abstoßen. Dies ermöglicht die Messung von Gleich- und Wechselströmen. Im oben erwähnten Artikel 6 zur Haupt-Schalttafel im Rittergut wurde zu den Messgeräten Nr. 5 und 9 der "E-AG" erwähnt, dass auf der Skala "System Hummel" vermerkt ist. Diese zeichneten sich durch die sehr geringe Masse von lediglich 0,3 g Eisen für das drehbare Blech aus. Ob die Instrumente unseres Exponats so ausgestattet sind ist höchstwahrscheinlich, denn das Patent wurde Georg Hummel bereits 1884 erteilt.
zeigt mit der Anordnung und Form der Bleche in a) ein Mantelkern-, in b) ein Streifenkern-Messwerk. In einer Rundspule ist zentrisch ein drehbares Blech (1 ) angeordnet, welches beim Mantelkern-Messwerk von einem feststehenden Blech (2 ) umgeben ist bzw. dem beim Streifenkern-Messwerk ein feststehender Blechstreifen (2 ) gegenüber steht. Das drehbare Blech ist mit der Zeigerachse verbunden. Durch den die Rundspule durchfließenden Strom werden in jedem Messwerk beide Bleche gleichsinnig magnetisiert, sodass sie sich voneinander abstoßen. Dies ermöglicht die Messung von Gleich- und Wechselströmen. Im oben erwähnten Artikel 6 zur Haupt-Schalttafel im Rittergut wurde zu den Messgeräten Nr. 5 und 9 der "E-AG" erwähnt, dass auf der Skala "System Hummel" vermerkt ist. Diese zeichneten sich durch die sehr geringe Masse von lediglich 0,3 g Eisen für das drehbare Blech aus. Ob die Instrumente unseres Exponats so ausgestattet sind ist höchstwahrscheinlich, denn das Patent wurde Georg Hummel bereits 1884 erteilt.
Die Begriffe Shunt und Vorwiderstand sind schnell erklärt:
- Mit Shunt oder auch Nebenwiderstand ist ein parallel zum Drehspulmesswerk angeordneter Widerstand definierter Größe in Ohm gemeint, an dem durch den fließenden Strom bedingt eine mit häufig nur 60 oder 150 mV (1 Millivolt = 0,001 V) kleine Spannung abfällt, die durch das Drehspulmesswerk gemessen und in Ampere angezeigt wird.
- Mit Vorwiderstand ist ein in Reihe mit dem Messgerät liegender Widerstand definierter Größe in Ohm gemeint, an dem der größte Teil der zu messenden Spannung abfällt und welche dann insgesamt in Volt angezeigt wird.
Mit Strom- und Spannungswandlern für Wechselstrom ist es ähnlich. Prinzipiell sind sie Transformatoren mit sehr genauen Übersetzungsverhältnissen:
- Mit Stromwandler ist ein Gerät gemeint, welches einen Strom bis in den Kiloamperebereich in eine handelbare Größe wie 1 oder 5 A umwandelt und dann auf einem Dreheisen-Messgerät anzeigt bzw. in einem Schutzgerät bei Überschreiten einer einstellbaren Grenze den Stromkreis bis in den Kilovoltbereich (z.B. 400 kV in unseren europaweiten Übertragungsnetzen) abschaltet.
- Mit Spannungswandler ist für die Spannung das Gleiche gemeint, er überträgt z.B. unsere Verteilnetz-Spannung von 110 oder 20 kV in eine handelbare Größe von 100 V.
7. Kapazitäts-, Leistungs- und Kurzschlussstromberechnung der Blei-Akkumulatoren
Weitere wichtige, noch in knapper Form zu erläuternde Themen des Blei-Akkumulators sind seine Kapazität, welche üblicherweise in Amperestunden (Ah), unter Einbeziehung der Akkuspannung nach Reihenschaltung mehrerer Zellen auch die Arbeit (Energie) in Kilowattstunden (kWh) oder als Leistung in Kilowatt (kW) und sein Kurzschlussstrom in Ampere (A) bzw. in Kiloampere (kA). Zunächst zu den Entlade- und Ladeströmen im Akku:
Otto Lueger geht hier in seinem bereits im Artikel "8. Die Akkumulator-Anlagen des »Ritterguts Züschen«" zitierten mehrbändigen Werk "Lexikon der gesamten Technik und ihrer Hilfswissenschaften" aus 1904 zunächst allgemein auf Akku-Ströme ein und nennt damalige Grenzwerte (extrem verkürztes Zitat, Quelle*4):
"Die zur Ladung und Entladung eines Akkumulators anzuwendende Stromstärke ….. richtet sich, abgesehen von den Besonderheiten der Plattenkonstruktion, nach der Größe der in dem Elemente vorhandenen Oberfläche der Platten einer Art. Es kommt nämlich darauf an, daß die auf die Flächeneinheit (z.B. 1 qdcm) der Plattenoberfläche entfallende Stromstärke ein gewisses Maß nicht überschreite. Man bezeichnet diese auf die Flächeneinheit bezogene Stromstärke als Stromdichte. ….. Bei der Entladung geht man bis etwa 1,0 (d.h. also 1 Ampere für jedes Quadratdezimeter), bei der Ladung bis etwa 0,8 Stromdichte. Bei Zulassung dieser Werte würde somit ein Akkumulator von 25 qdcm Oberfläche der positiven Platten im Maximum mit 25 × 1 = 25 Ampère entladen und mit 25 × 0,8 = 20 Ampère geladen werden dürfen. ….. Die Leistungsfähigkeit eines Akkumulators ist …..bedingt ….. durch das Produkt Stromstärke mal Zeit ….., die sogenannte Strommenge, in Ampèrestunden, bezeichnet ….. als Kapazität desselben. ….. Wenn der oben angenommene Akkumulator seinen Entladestrom von 25 Ampere 3 Stunden lang zu liefern vermag, so beträgt sonach seine Kapazität 3 × 25 = 75 Ampèrestunden."
 So einfach, aber auch extrem verkürzt, dies hier wiedergegeben wird, so schwierig stellt es sich bei der Bewertung der positiven Elektroden aus dem "Rittergut Züschen" dar: Wie ermittelt man die wirksame Oberfläche einer Platte aus den Abmessungen: Breite 170 mm, Höhe 180 mm, Stärke ca. 8 mm, zwei Seiten zu den negativen Elektrodenplatten rechts und links, hinzu noch vier Kantenflächen, zum Schluss drei positive Platten einer Elektrode (Bild rechts bzw. oben)? Mit diesen Fragen ist das Problem noch längst nicht komplett erfasst, wie Otto Lueger auf dem Weg zur komplexen Vielfalt beschreibt (Zitat, Quelle*4):
So einfach, aber auch extrem verkürzt, dies hier wiedergegeben wird, so schwierig stellt es sich bei der Bewertung der positiven Elektroden aus dem "Rittergut Züschen" dar: Wie ermittelt man die wirksame Oberfläche einer Platte aus den Abmessungen: Breite 170 mm, Höhe 180 mm, Stärke ca. 8 mm, zwei Seiten zu den negativen Elektrodenplatten rechts und links, hinzu noch vier Kantenflächen, zum Schluss drei positive Platten einer Elektrode (Bild rechts bzw. oben)? Mit diesen Fragen ist das Problem noch längst nicht komplett erfasst, wie Otto Lueger auf dem Weg zur komplexen Vielfalt beschreibt (Zitat, Quelle*4):
"Für manche Zwecke werden Akkumulatoren mit ganz kurzen Entladezeiten bis herab zu einer Stunde verlangt. Hierfür fertigen einige Fabriken entsprechende Typen an, bei denen die Stromdichte für einstündige Entladung bis zu 2,5 und für zweistündige Ladung bis zu 1,7 ansteigen kann. Daß man so hohe Stromdichten ohne Schaden anwenden kann, ist nur dadurch gelungen, daß man die eigentlich »wirksame Oberfläche« der Platten, d.h. die Berührungsfläche zwischen dem Bleikern, der aktiven Masse und der Säure, bei gleichbleibenden äußeren Abmessungen einer Platte, beträchtlich vergrößert hat. Dies hat man in der Weise zu erreichen gesucht, daß man den rohen Bleiplatten durch Anbringen einer möglichst großen Anzahl von Rinnen, Löchern, Hohlräumen u. dergl. eine größere Oberfläche gegeben hat, als dies früher geschehen war."
Extrem schwierig, weil von den zahlreichen Herstellern völlig unterschiedliche Verfahren angewandt wurden, um die wirksame Fläche der Platten zu vergrößern: Kräftige Rillen bis auf den letzten verbliebenen Millimeter in der Plattenstärke, unterschiedlichste Bohrungen von einer oder zwei Seiten mit verbliebener Rest-Plattenstärke, Querstreben unterschiedlichster Breite und Stärke zur Stabilisierung, usw. usw! Das Oberflächenfoto von einer der drei Platten der einzigen vorhandenen positiven Elektrode auf dieser Seite zeigt nur einen Teil der Problematik.
 Die vergrößerte Makroaufnahme links bzw. oben, hier um 90° gedreht, zeigt einen Ausschnitt aus der 17 cm breiten und 18 cm hohen Original-Platte gemäß obigem Foto. Bei insgesamt ausgezählten 114 Stegen von links nach rechts sind dort mit linkem und rechtem Plattenrand 113 Rillen zu erkennen, hier von oben nach unten. Dies bedeutet, dass Stege wie auch Rillen gemittelt etwa 0,75 mm Breite haben. Aber wie tief gehen die Rillen in die ca. 8 mm starke Platte hinein. Geschätzt haben wir dies mit 2,5 mm und dabei die horizontalen Stege vernachlässigt. Bei einer 180 mm hohen Platte mit gemittelt 0,75 mm breiten Rillen haben diese eine linke wie auch eine rechte Seite. Bei einer Plattenbreite von 170 mm entsteht also je Rille links wie rechts eine Oberfläche von je
Die vergrößerte Makroaufnahme links bzw. oben, hier um 90° gedreht, zeigt einen Ausschnitt aus der 17 cm breiten und 18 cm hohen Original-Platte gemäß obigem Foto. Bei insgesamt ausgezählten 114 Stegen von links nach rechts sind dort mit linkem und rechtem Plattenrand 113 Rillen zu erkennen, hier von oben nach unten. Dies bedeutet, dass Stege wie auch Rillen gemittelt etwa 0,75 mm Breite haben. Aber wie tief gehen die Rillen in die ca. 8 mm starke Platte hinein. Geschätzt haben wir dies mit 2,5 mm und dabei die horizontalen Stege vernachlässigt. Bei einer 180 mm hohen Platte mit gemittelt 0,75 mm breiten Rillen haben diese eine linke wie auch eine rechte Seite. Bei einer Plattenbreite von 170 mm entsteht also je Rille links wie rechts eine Oberfläche von je
170 mm * 2,5 mm = 425 mm2, für beide Flächen einer durchgehenden Rille also 850 mm2. Bei durchgehenden 113 Rillen sind dies für die vordere und hintere Seite einer Platte zusammen 113 * 2 * 850 mm2 = 192.100 mm2, bei drei Platten mit je zwei Seiten werden daraus also 3 * 192.100 mm2 = 576.300 mm2. Die verbleibenden horizontalen Stege und die Fläche im Untergrund der Rillen stellen auch eine wirksame Oberfläche dar, können also am einfachsten über die Oberfläche der sechs Plattenseiten mit 6 * 170 mm * 180 mm = 183.600 mm2 erfasst werden. In Summe sind dies also 759.900 mm2, 7.599 cm2, aufgerundet 76 dm2 oder auch 0,76 m2. Der Akku hätte also bei der oben genannten zulässigen und der zeitgenössischen Literatur entnommenen Stromdichte von 1A/dm2 mit 76 A entladen werden können, was bei einer Akkuspannung von 110 V einer Leistung von knapp 8,4 kW entspricht. Aber wie lange hätte er mit dieser Leistung entladen werden können?
Vor der Entladung kommt die Ladung und hier – der gleichen Literatur entnommen – mit 0,8 A/dm2, also knapp 61 A. Dies wäre sowohl für einen ersten Gleichstrom-Dynamo in der "Wilhelmsmühle" als auch für denselben Gleichstrom-Dynamo am DS-/GS-Umformersatz möglich gewesen, nicht jedoch für den späteren, hier ausgestellten Dynamo am Umformersatz im Rittergut! Es standen nach dem erhalten gebliebenen Leistungsschild des früheren Gleichstrom-Dynamos, angebracht an der Palette des DS-/GS-Umformersatzes neben den Kurzhinweisen, mit 116 A bei 146 V eine Gleichstromleistung von knapp 17 kW für alle Zellen in der "Wilhelmsmühle" zur Verfügung, nicht jedoch bei nur 12,5 kW Antriebsleistung des Drehstrom-Asynchronmotors am DS-/GS-Umformersatz im Rittergut. Beim hier als Exponat ausgestellten Dynamo mit 29 A bei 160 V stand im Rittergut nur eine Gleichstromleistung von 4,6 kW zur Verfügung. Damit wäre eine Aufladung beider Akkuanlagen mit je 66 Zellen in der "Wilhelmsmühle" nur über längere Zeit möglich, z. B. also auf je 120 Amperestunden (Ah) in insgesamt acht Stunden in der Mühle, alternativ in erheblich längerer Zeit parallel mit dem Verbrauchernetz je nach dessen Belastung. Die entscheidenden Fragen sind aber:
Welches Speichervermögen hat der obere Stauweiher vor der "Wilhelmsmühle" mit einem höchsten Oberwasserspiegel 203,667 m ü.N.N. (OW-Spiegel) bis zum Erreichen des tiefsten OW-Spiegels von 203,037 m ü.N.N., also einem zulässigen Absenken von 0,63 m, bei einer Entnahme von 0,565 m3/s (Quelle *5)?
Diese Frage kann recht genau beantwortet werden. Zwar ist aus den wasserrechtlichen Genehmigungsanlagen von 1934 das nutzbare Wasservolumen nicht zu entnehmen, angegeben ist jedoch eine Oberfläche des oberen Stauweihers vor der Wilhelmsmühle mit 9.700 m2 (Quelle *6). Bei einer nutzbaren Höhendifferenz von 0,63 m ergibt sich somit ein Wasservolumen von 6.111 m3, welches bei einer Maximalentnahme von 0,565 m3/s für eine Volllastbetriebszeit von 10.816 Sekunden entsprechend 3,0 Stunden reichen würde, das gespeicherte Wasser also "abgemahlen" ist. Bei einer Generator-Wirkleistung von 16 kW ergäbe das eine maximal nutzbare Energie von 48 kWh.
Zum Begriff "Abmahlen": Dies war seinerzeit der übliche Ausdruck bei der Nutzung aufgestauten Wassers durch Wasserräder bzw. -turbinen, bei Fachleuten ist er immer noch gebräuchlich. Er kommt vermutlich von einer der ersten Aufgabe einer Mühle, nämlich der Getreide-Vermahlung.
Welche Leistung haben die Turbine und der Generator nach einem Absinken auf den tiefsten Oberwasserspiegel bei einem festgestellten und nutzbaren Minimalzufluss von 150 Litern pro Sekunde, welcher eine Wasserentnahme in den Mühlgraben sowohl ohne als auch mit Aufstau ermöglicht?
Wenn der minimale Zufluss von 0,15 m3/s nach Erreichen des tiefsten OW-Spiegels sofort "abgemahlen" würde, betrüge die Leistung der Turbine bei einer wirksamen Fallhöhe von 4,80 m rechnerisch nur 6,3 kW. Jedoch wird auch der angenommene Wirkungsgrad von 0,9 entspr. Abschnitt 1 bei diesem geringen Zufluss deutlich sinken und die Turbinenleistung evtl. nur 4 kW betragen, die Generatorleistung noch weniger.
Bei einem Zufluss von lediglich 0,15 m3/s würden für ein Stauweiher-Volumen von 6.111 m3 für Vollstau zwar immerhin 40.740 Sekunden benötigt, aber das sind nur 11,3 Stunden. Der beratende Ingenieur Heinrich Leithäuser hat - alle Achtung - hervorragend geplant: Nach drei Stunden "Abmahlen" unter Volllast ist innerhalb eines halben Tages der obere Stauweiher wieder gefüllt!
Was ist bei zugefrorener "Elbe"?
Nach Entladung beider Akkus bleiben nur Kienspan, Kerze und Ölfunzel. Dies gilt theoretisch auch für den aktuellen PV-Insel-Wechselrichter des Autors nach langanhaltendem Netzausfall und "abgemahlenem" 6,5-kWh-Speicher. Aber er wohnt im Netzgebiet eines Versorgers, der bekannt ist für seine im Bundesgebiet vergleichsweise extrem kurzen Netzausfallzeiten, gerechnet je angeschlossenem Letztverbraucher!
Welche Gleichstromenergie in Kilowattstunden wird im Schloss und Rittergut bei 110 V für welche Zeit bei täglicher Ladung beider Akkuanlagen benötigt?
Für Beleuchtung war seinerzeit üblich eine Glühlampe zu 16 Normal-Kerzen (NK), orientiert an der früher üblichen Leuchtkraft einer "Normal-" oder auch "Hefner-Kerze". 16 NK entsprachen etwa 50 W einer früheren Glühfadenlampe, die Einheit NK bzw. HK selbst einer Lichtstärke von 0,903 cd (Candela). Wenn zunächst das "Schloss Garvensburg" im Winter nicht bewohnt war, Beleuchtung also i.W. nur im Sommerhalbjahr für wenige Stunden täglich benötigt wurde, erscheint eine weitere Betrachtung unnötig, denn jede Lampe zu 50 W benötigt bei 110 V einen Strom von 0,45 A, 20 Lampen also 9 A und damit wären z.B. die genannten 80 Ah erst in 8,9 Stunden entladen gewesen und entsprächen einem Verbrauch von etwa 8,8 kWh. Damit wären bei zugefrorener Elbe etwa acht bis neun Tage für die Beleuchtung möglich gewesen, bei Minimalzufluss hätte es keine Einschränkung gegeben! Otto Lueger schreibt dazu in seinem Lexikon aus 1904 (Zitat, Quelle *4):
"Bei der Ladung und Entladung dürfen die zulässigen Maximalwerte der Stromstärke ohne Schädigung der Platten nicht überschritten werden; dagegen kann man jeden Akkumulator mit beliebig geringeren Stromstärken entladen oder laden. ….. Außerdem bleibt die dazu erforderliche Strommenge (Stromstärke mal Zeit) nicht genau dieselbe, sondern man findet, daß sie bei abnehmender Stromdichte wächst. Ein Akkumulator ist also imstande, wenn man ihn beispielsweise mit der Hälfte des zulässigen Maximalstromes entladet oder ladet, eine größere Strommenge abzugeben bezw. aufzunehmen, als bei Anwendung der Maximalwerte, d.h. die Kapazität läßt sich durch Verminderung der Stromdichte erhöhen (gleichen prozentischen Betrag des Spannungsabfalls bei der Entladung vorausgesetzt). Es rührt dies daher, daß in letzterem Falle ein größerer Teil der vorhandenen aktiven Masse an den chemischen Umwandlungen bei Ladung und Entladung teilnimmt, als wenn man die Elemente mit höheren Stromdichten betreibt. So ist es möglich, durch Verminderung der Stromdichte um 25 bezw. 50% die Kapazität um etwa 20–50% zu steigern. Bei Anwendung der zurzeit verwendeten Stromdichten erfolgt die normale Entladung eines Akkumulators in etwa 3 Stunden, die Ladung in etwa 4 Stunden. Für manche Zwecke wird jedoch eine Entladung während längerer Zeitdauer (5, 7, 10 Stunden), also mit geringerer Stromdichte gewünscht, und man kommt dann, bei gleicher Leistung in Amperestunden, mit einer um so kleineren Plattenoberfläche aus, in je längerer Zeit die Entladung erfolgen soll."
Der Elektro-Energiebedarf von Schloss und Rittergut stieg zweifellos an, als Sohn Wolfgang, der ältere der beiden Söhne von Vater Wilhelm von Garvens-Garvensburg (Käufer des "Rittergutes Züschen" und Erbauer der "Wilhelmsmühle" sowie des "Schlosses Garvensburg"), seinen Wohnsitz nach Züschen verlegte, um sich der Land- und Forstwirtschaft zu widmen. Angenommen, der hier ausgestellte Umformersatz wäre mit 25 A insgesamt 10 Stunden täglich nacheinander oder abwechselnd nur für beide Akkuladungen betrieben worden, wären dies 250 Ah und bei 120 V eine eingespeiste Energie von 30 kWh, davon seinerzeit unter Berücksichtigung eines Wirkungsgrades von 80 % etwa 24 kWh nutzbar (Zitat, Quelle *4):
"Beim Laden eines Akkumulators wird Energie aus der Form elektrischer Arbeit in chemische Arbeit umgewandelt, während bei der Entladung die umgekehrte Umwandlung erfolgt. Da nun bei jeder derartigen Umsetzung von Energie Verluste stattfinden dadurch, daß ein Teil derselben in eine andre als die gewünschte Form (z.B. in Wärme) übergeht, so kann man wegen derartiger Verluste bei der Entladung nicht dieselbe Menge elektrischer Energie wieder erhalten, die man zur Ladung aufgewendet hat. ….. . Einerseits erhält man bei der Entladung nicht die ganze (in Ampèrestunden ausgedrückte) Strommenge wieder, die man hineingeladen hat, und es beträgt das Güteverhältnis bezüglich dieser Strommengen bei guten Akkumulatoren und den obengenannten maximalen Stromdichten zurzeit etwa 0,93–0,95, d.h. man erhält bei der Entladung 93–95% der zum Laden aufgewendeten Amperestunden wieder, vorausgesetzt, daß die Entladung unmittelbar oder doch innerhalb weniger Stunden auf die Ladung folgt. Anderseits ist aber auch die Klemmenspannung während der Entladung im Durchschnitt erheblich geringer als während der Ladung (vgl. die bezüglichen früheren Angaben). Die elektrische Arbeit aber ist bei der Ladung sowohl wie bei der Entladung in jedem Augenblicke gegeben durch das Produkt Klemmenspannung mal Stromstärke. Wird nun die letztere konstant gehalten, so erhält man die ganze bei der Ladung aufgewendete oder bei der Entladung gelieferte Arbeitsleistung, wenn man den konstanten Wert der Stromstärke mit dem Mittelwert der Klemmenspannung während der Ladung bezw. während der Entladung sowie mit der Zeitdauer multipliziert. Das Güteverhältnis dieser elektrischen Arbeitsmengen beträgt, da die mittlere Klemmenspannung während der Ladung 2,2–2,3 Volt, während der Entladung nur etwa 1,90 Volt ist, bei Anwendung hoher Stromdichten nicht viel über 80%. Bei geringeren Stromdichten stellt es sich günstiger und es können 85–87% erreicht werden. Das auf die elektrische Arbeitsleistung bezogene Güteverhältnis kommt praktisch allein in Betracht, da es maßgebend ist für die Leistung der zum Laden verwendeten Dynamomaschine und bei der Entladung für die praktisch nutzbare Leistung des Akkumulators. Für den praktischen Betrieb, der mancherlei Unregelmäßigkeiten mit sich bringt, kann man im Durchschnitt einen höheren Wirkungsgrad als 75–80% nicht annehmen."
Das dürfte zur damaligen Zeit für die wenigen mit Gleichstrom betriebenen Geräte völlig ausgereicht haben, die landwirtschaftlichen Maschinen wurden tagsüber durch Drehstrom versorgt. Resümee: Die Akkuanlagen waren aus Sicht des Energiebedarfs vermutlich überdimensioniert. Wie lange dann die Akkuanlagen z.B. im Winter bei zugefrorener "Elbe" noch Strom liefern konnten, ist nicht bekannt. Und ob schon nach 1920, dem Jahr des Anschlusses von Züschen an die öffentliche Stromversorgung, das "Schloss Garvensburg", das "Rittergut Züschen" und ggf. auch die "Wilhelmsmühle" mit ihrem Sägebetrieb – alle im nicht synchronisierter Inselbetrieb der Eigenerzeugung – an die VEW Waldeck angeschlossen wurden, ist auch nicht belegt. Aus dem erhaltenen Schriftwechsel geht nur die Stilllegung der eigenen Elektro-Energieerzeugung in 1962 hervor.
Nun zum Kurzschlussstrom des Blei-Akkumulators in Ampere (A) bzw. in Kiloampere (kA) mit einer Erläuterung zum sehr niedrigen Innenwiderstand und den dadurch bedingten extrem hohen Kurzschlussströmen. Denn die wirksame Oberfläche für die Akku-Kapazität hat auch Bedeutung für den Innenwiderstand (Zitat, *4):
"Der innere Widerstand des Akkumulators hat seinen Sitz vorwiegend an der Oberfläche der Elektrodenplatten, während nur der kleinere Teil desselben durch die Säureschichten zwischen den Platten gebildet ist. Er ist jedoch ….. sehr gering und beträgt schon bei kleinen Zellen von weniger als 10 qdcm Oberfläche der Platten einer Art, nicht über 0,01 Ohm und nimmt in demselben Verhältnis ab, in dem man die Plattenoberfläche vergrößert. Nach Ayrton kann man während der Entladung für jedes Quadratdezimeter Oberfläche der positiven Platten einen Widerstand von im Mittel etwa 0,08 Ohm rechnen. Danach hat ein Element von 20 qdcm Oberfläche den 20. Teil dieses Widerstandes, also etwa 0,004 Ohm, ein Element von 100 qdcm nur etwa 0,0008 Ohm."
Für die heutige Zeit ist der Gebrauch der ehemals häufigen Maßeinheit "Quadratdezimeter (qdcm)" sehr ungewöhnlich, es handelt sich also um eine Fläche mit einer Kantenlänge von jeweils 10 cm im Quadrat. Die drei positiven Platten einer Zelle haben bei einer Grundfläche von 17 cm Breite und 18 cm Höhe je eingehangene Platte aufgrund ihrer strukturierten, also wirksamen Oberfläche von ca. ??????
Das weiter oben abgebildete Exponat einer positiven Elektrode aus dem Rittergut Züschen mit 17 * 18 cm Kantenlänge, je zwei Seiten zu einer negativen Platte, drei Platten je Elektrode sowie vernachlässigter Oberflächenvergrößerung durch die Struktur und die Kanten hat ca. 18 dm2, das entspricht etwa 0,004 Ohm Innenwiderstand. Bei einer Zellenspannung von 2 V würde bereits ein Kurzschlussstrom über 500 A entstehen, bei den errechneten 76 dm2 (Errechnung s. weiter oben neben der Ausschnittvergrößerung) mit nur 0,001 Ohm aber bereits 2.000 A. Dies zwingt zur sicheren Verlegung und Anschlusstechnik.
8. Wirkungsweise eines Blei-Akkumulators
Erinnert sich der ein oder andere Leser dieses Abschnitts zur "Wirkungsweise eines Blei-Akkumulators" an den Chemieunterricht im Bereich "Anorganische Chemie"? Nein? So richtig auch der Autor nicht, die Elementbezeichnungen und ihre molekulare Bindung mit anderen Elementen hat er aber noch einigermaßen gut drauf. Daher wird hier ausschnittweise ein Wikipedia-Artikel wiedergegeben (Zitat, Quelle *5):
"Die Wirkungsweise des Bleiakkumulators lässt sich anhand der bei der Ladung und Entladung bzw. der Stromentnahme ablaufenden chemischen Prozesse darstellen. Bei der Entladung laufen nachfolgende chemische Vorgänge ab :
Negativer Pol:
Positiver Pol:
Beim Laden laufen die Vorgänge in Gegenrichtung ab, ...... . Die Gesamtreaktion beim Entladen und Laden:
Nach rechts findet unter Energieabgabe die Entladung des Bleiakkus statt, nach links unter Energiezufuhr die Aufladung. Aus der elektrochemischen Spannungsreihe kann man nun die Potentialdifferenz, also letztlich die elektrische Spannung, die entsteht, berechnen:
Selbstentladung
Blei(IV)-oxid ist in schwefelsaurer Lösung unbeständig."
Der Autor entnimmt daraus: Die hochgesetzten "2-" beim Schwefelsulfat (SO4) vor dem Rechtspfeil bedeuten wie die normal gesetzten "2e-" nach dem Pfeil beim negativen Pol die Freigabe von zwei negativ geladenen Elektronen, welche über die Leitung und den Verbraucher, z.B. eine Lampe, zum positiven Pol fließen. Dort entstehen aus der Schicht Blei(IV)-oxid (PbO2) auf dem reinen Blei (Pb), dem Schwefelsulfat SO4), den positiv geladenen vier Wasserstoffionen (H+) und den zwei negativ geladenen Elektronen (e-) das Bleisulfat (PbSO4) und zwei Wassermoleküle H2O. Im Artikel "7. Der Drehstrom-/Gleichstrom-Umformersatz des »Ritterguts Züschen«" wurde beim Gleichstrom-Motor im Zusammenhang mit dessen hohem, wie ein Kurzschluss wirkender Anlaufstrom die innere EMK (früher "Elektro-Motorische Kraft" genannt) erwähnt. Hier ist sie mit dem Begriff "E0Ges" als resultierende Gesamtspannung aus Blei (Pb) und Blei(IV)-oxid (PbO2) in Schwefelsulfat (SO4). Selbstentladung ist das große Problem des Bleiakkus, mit Sicherheit auch in Züschen über die Wintertage bei zugefrorener Elbe. Bei der Selbstentladung wird also Wasserdampf und Sauerstoff freigesetzt.
Text und nicht besonders gekennz. Bilder: Wolfgang Dünkel, VDE Kassel u. TMK
(last update 04.08.2025)
Hier finden Sie eine verlinkte Auflistung unserer seit Oktober 2020 vorgestellten Objekte des Monats.
--------------------------------------------------------------------------------
Grafik-, Bild- und Textquellen bzw. -zitate:
*1: Helmut Lotz, VDE Kassel und TMK
*2: Michael von Dolivo-Dobrowolsky und der Drehstrom, Geschichte der Elektrotechnik 19, VDE Verlag GmbH, Berlin, Offenbach, ISBN 3-8007-2779X, S. 118
*3: Drehspul-/Dreheisenmesswerk, Franz Moeller VDE, Leitfaden der Elektrotechnik , Band IV, Stöckl, Winterling, Elektrische Messtechnik, 4. Auflage, 1968, B.G. Teubner Verlagsgesellschaft, Stuttgart, Seiten 23, 39
*4: Akkumulatoren für Elektrizität, Otto Lueger, Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Stuttgart, Leipzig 1904, Bd. 1, S. 109 – 115, gefunden bei Zeno.org, gemeinfrei
*5: Oberwasserspiegel, Zeichnung 10279, Blatt 7, und Anlage 1 der Sicherstellungs-und Verleihungsurkunde, HStAM, Best. 401,35, Nr. W1006
*6: Speichervermögen, Anlage 1 der Sicherstellungs-und Verleihungsurkunde vom 18. Mai 1934, Seite 4, Punkt 7, HStAM, Best. 401,35, Nr. W1006
*X: Bleiakkumulator, Bleiakkumulator – Wikipedia








